This chapter contains some mathematical background needed to discuss cryptography, which is the topic of the next chapter. In particular, we will be reviewing modular arithmetic, which we assume you are already familiar with. We’ll remind you the basic definitions in this area as well as go over the computational complexities of the most common modular arithmetic operations. For cryptographic applications, we use the fact that some modular operations are efficiently computable, but also exploit the assumed computational hardness of other modular operations. Therefore, the distinction between which operations are efficiently computable and which ones are not is important to understand.
Let \(A, B \in \mathbb Z\). We say that \(A\) divides \(B\) (or \(A\) is a divisor of \(B\)), denoted \(A | B\), if there is a number \(C \in \mathbb Z\) such that \(B = AC\).
Let \(P \in \mathbb N\). We say that \(P\) is a prime number if \(P \geq 2\) and the only divisors of \(P\) are \(1\) and \(P\).
Let \(A, B\) and \(N\) be positive integers. We denote by \(A \bmod N\) the remainder you get when you divide \(A\) by \(N\). Note that \(A \bmod N \in \{0,1,2,\ldots,N-1\}\). We say that \(A\) and \(B\) are congruent modulo \(N\), denoted \(A \equiv_N B\) (or \(A \equiv B \bmod N\)), if \(A \bmod N = B \bmod N\).
Show that \(A \equiv_N B\) if and only if \(N | (A - B)\).
If \(A \equiv_N B\), then by definition, \(A\) and \(B\) have the same remainder \(R\) when they are divided by \(N\). So we can write \(A = Q\cdot N + R\) for some \(Q \in \mathbb Z\) and \(B = Q' \cdot N + R\) for some \(Q' \in \mathbb Z\). Then \(A-B = (Q - Q') \cdot N\), and therefore \(N | (A-B)\).
Suppose \(N | (A-B)\). Write \(A = Q \cdot N + R\) for some \(Q \in \mathbb Z\) and \(R \in \{0,1,\ldots, N-1\}\). Also write \(B = Q' \cdot N + R'\) for some \(Q' \in \mathbb Z\) and \(R' \in \{0,1,\ldots, N-1\}\). Then \(A - B = (Q - Q') \cdot N + (R - R')\). Since \(N | (A-B)\), it must be the case that \(N | (R - R')\). Since \(R-R'\) is an integer between \(-(N-1)\) and \((N-1)\), the only way \(N\) can divide \(R-R'\) is if \(R=R'\), i.e., \(A \equiv_N B\).
The above characterization of \(A \equiv_N B\) can be taken as the definition of \(A \equiv_N B\). Indeed, it is used a lot in proofs.
We write \(\gcd(A, B)\) to denote the greatest common divisor of \(A\) and \(B\). Note that for any \(A\), \(\gcd(A,1) = 1\) and \(\gcd(A, 0) = A\).
We say that \(A\) and \(B\) are relatively prime if \(\gcd(A,B) = 1\).
In the section below, we first give the definitions of basic modular operations like addition, subtraction, multiplication, division and exponentiation. We also explore some of their properties. In the section after, we look at the computational complexity of these operations. Being able to compute these operations efficiently is crucial for applications.
We let \(\mathbb Z_N\) denote the set \(\{0,1,2,\ldots,N-1\}\).
For \(A, B \in \mathbb Z_N\), we define the addition of \(A\) and \(B\), denoted \(A +_N B\), as \((A+B) \bmod N\). When \(N\) is clear from the context, we can drop the subscript \(N\) from \(+_N\) and write \(+\). For \(N=5\), we can represent the addition operation in \(\mathbb Z_5\) using the following table.

In \(\mathbb Z_N\), the element 0 is called the additive identity. It has the property that for any \(A \in \mathbb Z_N\), \(A +_N 0 = 0 +_N A = A\).
Show that if \(A \equiv_N B\) and \(A' \equiv_N B'\), then \(A+ A' \equiv_N B+B'\).
Show that for any \(A,B \in \mathbb Z\), \[(A + B) \bmod N = (A \bmod N) +_N (B \bmod N).\]
Part 1: Since \(A \equiv_N B\), we have \(N | (A-B)\), and since \(A' \equiv_N B'\), we have \(N | (A'-B')\). This implies \(N | (A-B) + (A'-B')\), or in other words, \(N | (A+A') - (B+B')\). And this is equivalent to \(A + A' \equiv_N B + B'\).
Part 2: Follows from the previous part and the definition of \(+_N\).
Let \(A \in \mathbb Z_N\). The additive inverse of \(A\), denoted \(-A\), is defined to be an element in \(\mathbb Z_N\) such that \(A +_N -A = 0\).
Show that every element of \(\mathbb Z_N\) has a unique additive inverse.
The additive inverse of \(A \in \mathbb Z_N\) is \(0\) if \(A = 0\), and is \(N-A\) otherwise.
To show uniqueness, assume that \(-A\) and \(-A'\) are both additive inverses of \(A\). Then \(A +_N -A = A +_N -A' = 0\), which implies \(-A = -A'\).
Let \(A, B \in \mathbb Z_N\). We define “\(A\) minus \(B\)”, denoted \(A -_N B\), as \(A +_N -B\).
Show that in the addition table of \(\mathbb Z_N\), every row and column is a permutation of the elements \(\mathbb Z_N\).
We argue that every row contains distinct elements of \(\mathbb Z_N\), which implies that every row is a permutation of \(\mathbb Z_N\). Take an arbitrary row, which corresponds to some element \(A \in \mathbb Z_N\). Suppose for the sake of contradiction that two entries of this row are the same. Then there exists \(B\) and \(B'\) in \(\mathbb Z_N\), \(B \neq B'\), such that \(A +_N B = A +_N B'\). But then if we add \(-A\) to both sides of the equality, we get \(B = B'\), a contradiction.
The argument for the columns is the same.
For \(A, B \in \mathbb Z_N\), we define the multiplication of \(A\) and \(B\), denoted \(A \cdot_N B\), as \(AB \bmod N\). If \(N\) is clear from the context, we can drop the subscript \(N\) from \(\cdot_N\) and write \(\cdot\). Furthermore, we can even drop \(\cdot\) and represent \(A \cdot_N B\) as simply \(AB\).
Show that if \(A \equiv_N B\) and \(A' \equiv_N B'\), then \(AA' \equiv_N BB'\).
Show that for any \(A,B \in \mathbb Z\), \[AB \bmod N = (A \bmod N) \cdot_N (B \bmod N).\]
Part 1: Hint: Write the elements as \(QN + R\) for some \(Q \in \mathbb Z\) and remainder \(R \in \{0,1,\ldots,N-1\}\).
Part 2: Follows from Part 1 and the definition of \(\cdot_N\).
Let \(A \in \mathbb Z_N\). The multiplicative inverse of \(A\), denoted \(A^{-1}\), is defined to be an element in \(\mathbb Z_N\) such that \(A \cdot_N A^{-1} = 1\).
Let \(A,N \in \mathbb N\). The multiplicative inverse of \(A\) in \(\mathbb Z_N\) exists if and only if \(\gcd(A,N) = 1\).
Let \(A, B \in \mathbb Z_N\), where \(B\) has a multiplicative inverse \(B^{-1}\). Then we define “\(A\) divided by \(B\)”, denoted \(A /_N B\), as \(A \cdot_N B^{-1}\).
We let \(\mathbb Z_N^*\) denote the set \(\{A \in \mathbb Z_N : \gcd(A, N) = 1\}\). In other words, \(\mathbb Z_N^*\) is the set of all elements of \(\mathbb Z_N\) that have a multiplicative inverse.
Show that \(\mathbb Z_N^*\) is closed under multiplication, i.e., \(A,B \in \mathbb Z_N^* \implies A \cdot_N B \in \mathbb Z_N^*\).
If \(A\) and \(B\) are in \(\mathbb Z_N^*\), then they have inverses \(A^{-1}, B^{-1} \in \mathbb Z_N^*\). To show \(A \cdot_N B\) is in \(\mathbb Z_N^*\), we need to show that it has an inverse modulo \(N\). And indeed, \(B^{-1} \cdot_N A^{-1}\) is the inverse of \(A \cdot_N B\) since \(A \cdot_N B \cdot_N B^{-1} \cdot_N A^{-1} = 1\).
Similar to an addition table for \(\mathbb Z_N\), one can consider a multiplication table for \(\mathbb Z_N^*\). For example, \(\mathbb Z_8^* = \{1, 3, 5, 7\}\), and the multiplication table is as below:
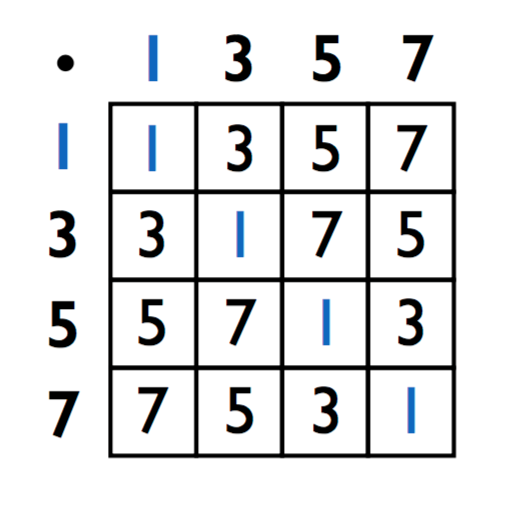
Show that in the multiplication table of \(\mathbb Z_N^*\), every row and column is a permutation of the elements \(\mathbb Z_N^*\).
We argue that every row contains distinct elements of \(\mathbb Z_N^*\), which implies that every row is a permutation of \(\mathbb Z_N^*\). Take an arbitrary row, which corresponds to some element \(A \in \mathbb Z_N^*\). Suppose for the sake of contradiction that two entries of this row are the same. Then there exists \(B\) and \(B'\) in \(\mathbb Z_N^*\), \(B \neq B'\), such that \(A \cdot_N B = A \cdot_N B'\). But then if we multiply both sides of the equality by \(A^{-1}\) we get \(B = B'\), a contradiction.
The argument for the columns is the same.
The Euler totient function \(\varphi : \mathbb N\to \mathbb N\) is defined as \(\varphi(N) = |\mathbb Z_N^*|\). By convention, \(\varphi(0) = 0\).
Show that for \(P\) a prime number, \(\varphi(P) = P-1\). Also show that for \(P\) and \(Q\) distinct prime numbers, \(\varphi(PQ) = (P-1)(Q-1)\).
We know that \(\varphi(N)\) is the number of elements in \(\{0,1,2,\ldots,N-1\}\) that are relatively prime to \(N\). If \(P\) is a prime number, then for any \(A \in \{1,2,\ldots,P-1\}\), we have \(\gcd(A,P) = 1\). And \(\gcd(0,P) = P\). So \(\varphi(P) = P-1\).
When \(N = PQ\) for distinct primes \(P\) and \(Q\), we need to determine the number of elements in \(\{0,1,2,\ldots,PQ-1\}\) that are relatively prime to \(PQ\). The elements that are not relatively prime to \(PQ\) are \(0\) and \[\begin{aligned} P, 2P, 3P, \ldots, (Q-1)P, \\ Q, 2Q, 3Q, \ldots, (P-1)Q.\end{aligned}\] In total there are \(1 + (Q-1) + (P-1) = Q + P - 1\) of these elements. Then the number of elements that are relatively prime to \(PQ\) is \(PQ - (Q + P - 1) = PQ - Q - P + 1 = (P-1)(Q-1)\).
Let \(A \in \mathbb Z_N\) and \(E \in \mathbb Z\). We write \(A^E\) to denote \[\underbrace{A \cdot_N A \cdot_N \cdots \cdot_N A}_{E \text{ times}}.\]
For any \(A \in \mathbb Z_N^*\), \(A^{\varphi(N)} = 1\). Equivalently, for any \(A,N \in \mathbb Z\) with \(\gcd(A,N) = 1\), \(A^{\varphi(N)} \equiv_N 1\).
(In this proof we drop the subscript \(N\) from the multiplication notation.) Take an arbitrary \(A \in \mathbb Z_N^*\). Let \(B_1,B_2,\ldots,B_k\) be the elements of \(\mathbb Z_N^*\), where \(k = \varphi(N)\). By Exercise (Multiplication table permutation property), \(\{AB_1, AB_2, \ldots, AB_k\} = \mathbb Z_N^*\). The product of all the elements in the first set can be written as \((AB_1)(AB_2)\cdots (AB_k)\). This must be equal to the product \(B_1B_2 \cdots B_k\), i.e. \[(AB_1)(AB_2)\cdots (AB_k) = B_1B_2\cdots B_k.\] Dividing both sides by \(B_1B_2\cdots B_k\) (i.e. multiplying both sides by the inverse of \(B_1B_2 \cdots B_k\)), we get \(A^k = 1\), as desired.
When \(N\) is a prime number, then Euler’s Theorem is known as Fermat’s Little Theorem.
Let \(A \in \mathbb Z_N^*\) and \(E \in \mathbb Z\). Show that \(A^E \equiv_N A^{E \bmod \varphi(N)}\).
We can write \(E = \varphi(N) \cdot Q + R\) where \(Q\) is some integer and \(R \in \{0,1,\ldots, \varphi(N)-1\}\) is the remainder. So \(E \equiv_{\varphi(N)} R\). Then \[A^E = A^{\varphi(N) \cdot Q + R} = \left(A^{\varphi(N)}\right )^Q \cdot A^R = A^R,\] where for the last equality, we used Euler’s Theorem.
Since \(\gcd(102,7) = 1\), we can use the previous exercise and reduce the exponent modulo \(6\). So \(102^{98} \equiv_7 102^2\). Furthermore, \(102\) can be reduced modulo \(7\). So \(102^{2} \equiv_7 4^2\). And \(16\) modulo \(7\) is \(2\), which is the answer.
What the previous two exercises demonstrate is that if we are exponentiating an element \(A \in \mathbb Z_N^*\), then we can effectively think of the exponent as living in the set \(\mathbb Z_{\varphi(N)}\). This will be important to keep in mind when we cover Cryptography later.
Let \(A \in \mathbb Z_N^*\). We say that \(A\) is a generator if \[\{A^E : E \in \mathbb Z_{\varphi(N)}\} = \mathbb Z_N^*.\]
If \(P\) is a prime number, then \(\mathbb Z_P^*\) contains a generator.
In this section, we will look at the computational complexities of doing the basic modular operations discussed in the previous section. We will use the fact that addition, subtraction, multiplication and division operations can be computed efficiently in \(\mathbb Z\). Note that \(A \bmod N\) is easy to compute by dividing \(A\) by \(N\) and seeing what the remainder is.
In order to compute \(A +_N B\) in \(\mathbb Z_N\), we can simply add \(A\) and \(B\) in \(\mathbb Z\) and then take the sum modulo \(N\). To compute \(A -_N B\), we can do \(A + (N-B)\) in \(\mathbb Z\) and then take the result modulo \(N\).
In order to compute \(A \cdot_N B\) in \(\mathbb Z_N\), we can multiply \(A\) and \(B\) in \(\mathbb Z\) and then take the product modulo \(N\). To compute \(A /_N B = A \cdot_N B^{-1}\), we first need to figure out whether \(B\) has a multiplicative inverse. Recall that \(B^{-1}\) exists if and only if \(B\) and \(N\) are relatively prime, i.e. \(\gcd(B,N) = 1\). The following algorithm, known as Euclid’s Algorithm, efficiently computes the greatest common divisor of two numbers.
\(\gcd(A, B)\):
If \(B = 0\), then return \(A\).
Else return \(\gcd(B, A \bmod B)\).
Show that if \(A \geq B\), \(\gcd(A,B) = \gcd(A-B, B)\). Use this to show that Euclid’s Algorithm correctly computes the greatest common divisor of two numbers.
If \(x\) divides \(A\) and \(B\), then it must divide \(A-B\). In particular, \(\gcd(A,B)\) divides both \(B\) and \(A-B\), and therefore \(\gcd(A-B,B) \geq \gcd(A, B)\).
If \(x\) divides \(A-B\) and \(B\), then it must divide \(A\). In particular, \(\gcd(A-B,B)\) divides both \(A\) and \(B\), and therefore \(\gcd(A,B) \geq \gcd(A-B, B)\).
So we can conclude \(\gcd(A,B) = \gcd(A-B,B)\).
When \(A \geq B\), if we iteratively use the equality \(\gcd(A,B) = \gcd(A-B,B)\) to subtract \(B\) from the larger number \(A\), then we will eventually arrive at \(\gcd(A,B) = \gcd(A \bmod B, B)\). For example: \[\begin{aligned} \gcd(6004, 6) & = \gcd(5998, 6) \\ & = \gcd(5992, 6) \\ & = \gcd(5986, 6) \\ & \cdots \\ & = \gcd(4,6).\end{aligned}\] So \(\gcd(6004, 6)\) eventually ends up at \(\gcd(6004 \bmod 6, 6)\).
\(\gcd(A \bmod B, B)\) is obviously equal to \(\gcd(B, A \bmod B)\). So one can show that Euclid’s algorithm is correct by an induction argument, where the base case corresponds to the base case of the recursive algorithm, and the induction step corresponds to the recursive call.
Suppose \(A\) and \(B\) can be represented with at most \(n\) bits each. Give an upper bound on the number of recursive calls Euclid’s Algorithm makes in terms of \(n\).
We claim that \(A \bmod B \leq A/2\). To see this, we case on whether \(A \geq 2B\). If \(A \geq 2B\), then the claim is true because \(A \bmod B\) is always less than \(B\). If \(A < 2B\), then the claim is true because \(A \bmod B = A - B < A - A/2 = A/2\).
Now when we call the algorithm with input \((A, B)\) and make a recursive call, the next pair of inputs is \((B, A \bmod B)\). Using the claim above, we have \((A \bmod B) \cdot B \leq A B/2\). So in each recursive call, the product of the inputs is going down by a factor of at least 2. And this implies the number of recursive calls is at most \(\log_2 (A B)\), which is \(O(n)\) if \(A\) and \(B\) are at most \(n\)-bits.
Using Euclid’s Algorithm, we can check if \(\gcd(B,N) = 1\) and determine if \(B\) has a multiplicative inverse. It turns out that a slight modification of Euclid’s Algorithm also allows us to compute \(B^{-1}\) if it exists. In order to show this, we first need a definition.
Let \(A,B,C \in \mathbb N\). We say that \(C\) is a miix of \(A\) and \(B\) if \[C = k A + \ell B\] for some \(k, \ell \in \mathbb Z\).
Let \(A,B,C \in \mathbb N\). Show that if \(C\) is a miix of \(A\) and \(B\) then \(C\) is a multiple of \(\gcd(A,B)\).
Let \(G = \gcd(A, B)\). If \(C\) is a miix of \(A\) and \(B\), then \(C = kA + \ell B\). Furthermore, we know we can write \(A = xG\) for some integer \(x\), and \(B = yG\) for some integer \(y\). Therefore \[C = kA + \ell B = kxG + \ell yG = G(kx + \ell y),\] which shows \(C\) is a multiple of \(G\).
Show how to extend Euclid’s algorithm so that it outputs \(k\) and \(\ell\) such that \(\gcd(A,B) = k A + \ell B\). Then conclude that if \(C\) is any multiple of \(\gcd(A,B)\), then \(C\) is a miix of \(A\) and \(B\).
Here is the extended Euclid’s algorithm.
\[\begin{aligned} \hline\hline\\[-12pt] &\textbf{def}\;\; \text{Extended-Euclid}(A,B):\\ &{\scriptstyle 1.}~~~~\texttt{If $B$ divides $A$, return $(B, 0, 1)$.}\\ &{\scriptstyle 2.}~~~~\texttt{Else:}\\ &{\scriptstyle 3.}~~~~~~~~(G,k,\ell) = \text{Extended-Euclid}(B, A \bmod B)\\ &{\scriptstyle 4.}~~~~~~~~\texttt{Return $(G,\ell, (k-\ell \cdot \lfloor A/B \rfloor ) )$}\\ \hline\hline\end{aligned}\]
Here, we have modified Euclid’s algorithm to return a tuple of variables; Extended-Euclid\((A,B) = (G,k,\ell)\) where \(G = \gcd(A,B)\) and \(G = k \cdot A + \ell \cdot B.\) By the correctness of Euclid’s algorithm, we can conclude that the returned value \(G\) is the gcd (both algorithms do the same calculations for \(G\)). We use induction on the number of steps to argue correctness of the returned values \((k,\ell).\)
Base Case: If \(B\) divides \(A\), the algorithm correctly returns \(k=0\) and \(\ell=1\).
Induction Step: Suppose the algorithm ran for \(s >1\) steps. By the induction hypothesis, we can assume that \(G = k \cdot B + \ell \cdot (A \bmod B).\) Since we can write \(A = q\cdot B + (A \bmod B)\) where \(q = \lfloor A/B \rfloor\), we can say \(G = k \cdot B + \ell (A - q\cdot B)\). Thus, the returned tuple \((G, \ell, k - \ell \cdot \lfloor A/B \rfloor)\) is correct.
The above algorithm shows that \(\gcd(A,B)\) is a miix of \(A\) and \(B\). So if \(C\) is a multiple of \(\gcd(A,B)\), it is also a miix of \(A\) and \(B\).
Suppose \(B\) has a multiplicative inverse modulo \(N\), i.e. \(\gcd(B,N) = 1\). Then by the previous exercise, we can obtain \(k\) and \(\ell\) such that \(1 = kB + \ell N\). If we take this equation modulo \(N\), we get that \(kB \equiv_N 1\). Therefore \(k\) is the multiplicative inverse of \(B\).
To sum up, if we want to compute \(A /_N B = A \cdot_N B^{-1}\), we can first compute \(B^{-1}\) and then compute \(A \cdot_N B^{-1}\).
Prove Proposition (Multiplicative inverse characterization) using the previous two exercises.
The previous two exercises imply that \(C\) is a miix of \(A\) and \(B\) if and only if \(C\) is a multiple of \(\gcd(A,B)\). Then, \[\begin{aligned} A^{-1} \text{ exists } & \Longleftrightarrow \; \exists k \text{ such that } k A \equiv_N 1 \\ & \Longleftrightarrow \; \exists k \text{ such that $N$ divides $kA - 1$ } \\ & \Longleftrightarrow \; \exists k, q \text{ such that } k A - 1 = qN \\ & \Longleftrightarrow \; \exists k, q \text{ such that } 1 = kA + (-q)N \\ & \Longleftrightarrow \; \text{1 is a miix of $A$ and $N$} \\ & \Longleftrightarrow \; \gcd(A,N) = 1.\end{aligned}\]
Given \(N \in \mathbb N\), \(A \in \mathbb Z_N\) and \(E \in \mathbb N\), we can compute \(A^E \bmod N\) efficiently. Assume that \(A, E\) and \(N\) can be represented using at most \(n\) bits each. The algorithm below is known as fast modular exponentiation. To understand how the algorithm works, see the example following the algorithm.
\(\text{FME}(A, E, N)\):
Repeatedly square \(A\) to obtain
\(A^2 \bmod N\), \(A^4 \bmod N\), \(A^8 \bmod N\), \(\ldots\), \(A^{2^n} \bmod N\).Multiply together (modulo \(N\)) the powers of \(A\) so that the product is \(A^E\).
To figure out which powers to multiply, look at the binary representation of \(E\).
Consider the example of computing \(2337^{53} \bmod 100\). The first step of the algorithm computes \[\begin{aligned} 2337^{2} \bmod 100 \\ 2337^{4} \bmod 100 \\ 2337^{8} \bmod 100 \\ 2337^{16} \bmod 100 \\ 2337^{32} \bmod 100 \end{aligned}\] by squaring \(2337\) modulo \(100\) \(5\) times. The binary representation of \(53\) is \(110101\). This implies that \[53 = 1 + 4 + 16 + 32.\] Therefore to calculate \(2337^{53} \bmod 100\), the second step of the algorithm does: \[(2337 \bmod 100) \cdot (2337^{4} \bmod 100) \cdot (2337^{16} \bmod 100) \cdot (2337^{32} \bmod 100).\]
Suppose \(A, E\) and \(N\) are integers that can be represented using at most \(n\) bits. Give an upper bound on the running time of the above algorithm in terms of \(n\).
Consider the following computational problem. You are given \(A, E, N \in \mathbb N\) with \(A \in \mathbb Z_N^*\). The goal is to output \(B \in \mathbb N\) such that \(B^E \equiv_N A\). In other words, the goal is to find the \(E\)’th root of \(A\) in \(\mathbb Z_N^*\) (if it exists). Many experts believe (but cannot prove) that this problem cannot be computed in polynomial time. The assumed hardness of this problem is used in the famous RSA cryptosystem (see the chapter on Cryptography for details).
Consider the following computational problem which is known as the Discrete Log Problem in \(\mathbb Z_P^*\). You are given \(A, B, P \in \mathbb N\), where \(P\) is a prime number, \(A \in \mathbb Z_P^*\), and \(B \in \mathbb Z_P^*\) is a generator (Theorem (\(\mathbb Z_P^*\) contains a generator) tells us that \(\mathbb Z_P^*\) always contains a generator). The goal is to output \(X \in \mathbb N\) such that \(B^X \equiv_P A\). In a sense, this is like trying to compute \(\log_B A\) in \(\mathbb Z_N^*\). Many experts believe (but cannot prove) that this problem cannot be computed in polynomial time. The assumed hardness of this problem is used in the famous Diffie-Hellman secret key exchange protocol (see the chapter on Cryptography for details).
Wilson’s theorem states that \(N\) is prime if and only if \((N-1)! \equiv_N N-1\). Can we use this fact in the obvious way to design a polynomial time algorithm for isPrime?
True or false: Suppose that \(A^K \equiv_N 1\), where \(A \neq 1\). Then \(\varphi(N) | K\).
Determine, with proof, \(750^{10002} \pmod{251}\). Note that \(251\) is prime.
Determine, with proof, \(251^{(15^{251})} \pmod{7}\).
Let \(G\) be a generator in \(\mathbb Z_N^*\), and let \(R \in \mathbb Z_{\varphi(N)}\) be chosen uniformly at random. For every \(A \in \mathbb Z_N^*\), determine \(\Pr[G^R = A]\).
Let \(R \in \mathbb Z_N^*\) be chosen uniformly at random. For every \(A, B \in \mathbb Z_N^*\), determine \(\Pr[A \cdot_N R = B]\).
What is Euler’s Theorem?
What is a generator in \(\mathbb Z_N^*\)?
Consider the addition, subtraction, multiplication, division, exponentiation, taking logarithm, and taking root. Which of these operations are known to be polynomial-time solvable when the universe is the integers? Which of them are known to be polynomial-time solvable in the modular universe?
What is an efficient algorithm for finding the multiplicative inverse of an element in \(\mathbb Z_N^*\)?
The theory behind modular arithmetic should mostly be review. It is important to know how the basic operations are defined and what kind of properties they have.
For which modular arithmetic operations do we have an efficient algorithm for (and what is that algorithm)? For which operations do we not expect to have an efficient algorithm? And for these operations, why don’t the “obvious” algorithms work? You should have a solid understanding of all these. Please internalize Important Note (Our model when measuring running time) and Important Note (Integer inputs are large numbers).