
This chapter is about mathematically formalizing mathematical reasoning itself, and in the process, discovering some of the fundamental properties of mathematics. We are going to refer to the usual mathematical reasoning (that mathematicians have engaged in for centuries) as “Good Old Regular Mathematics”, or \(\text{GORM}\) for short. So the goal is to build a mathematical model that captures \(\text{GORM}\), and then study that mathematical model.
\(\text{GORM}\) can be thought of as the following two processes.
\(\text{Prover}\): Given a statement \(S\), come up with a proof \(P\) of \(S\) (if it exists).
\(\text{Verifier}\): Given a statement \(S\) and an argument \(P\), verify whether \(P\) is a proof of \(S\).
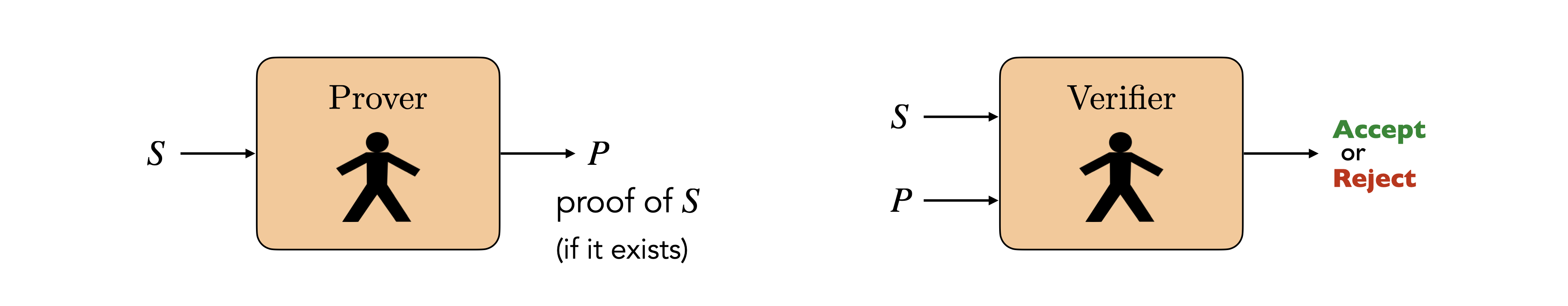
Given a Verifier, we can build a Prover as follows: try all possible arguments \(P\) one by one (e.g. in lexicographical order) and then using the Verifier, check if \(P\) is a proof of \(S\), and if it is, output \(P\). Granted this is not an efficient Prover, but the efficiency of the Prover will not play any role in the results presented in this paper.
All the elements of \(\text{GORM}\) that need to be formalized are captured by \(\text{Verifier}\), so we can just focus on it and make sure that we formalize all its pieces.
Note that both \(\text{Prover}\) and \(\text{Verifier}\) above represent computational processes. So a key part in formalizing \(\text{GORM}\) is the formalization of computation. Luckily, we already have a great model for computation: Turing machines.
Even though our main interest is formalizing all mathematical reasoning, it is useful to build a general framework for formalizing any subset of mathematical reasoning. For instance, we may want to come up with a formalization that captures mathematical reasoning for plane geometry. Or we may want to formalize basic arithmetic. Or we may want to formalize probability theory. For any area \(A\) of mathematical reasoning, we will let \(\text{GORM}_A\) denote Good Old Regular Mathematics restricted to \(A\). Without the subscript, \(\text{GORM}\) represents all mathematical reasoning.
Let \(A\) be some area of mathematics. A proof system \(\text{PS}_A\) for \(A\) is a mathematical formalization of \(\text{GORM}_A\) with the following properties.
For every statement \(S\) in \(\text{GORM}_A\) with a truth value, there is a precise representation of \(S\) in \(\text{PS}_A\).
For every argument \(P\) in \(\text{GORM}_A\), there is a precise representation of \(P\) in \(\text{PS}_A\).
\(\text{PS}_A\) specifies a decider TM \(V\) (called a verifier) such that \(V(\left \langle S,P \right\rangle)\) accepts if and only if \(P\) is a proof of \(S\).
Since the verification process represents a computation, there is an implicit requirement that the set of statements in \(\text{PS}_A\) as well as the set of proofs in \(\text{PS}_A\) are encodable.
Below is some standard terminology that we will be using regarding statements in a proof system.
Let \(\text{PS}\) be a proof system and let \(S\) be a statement in \(\text{PS}\).
Statement \(S\) is provable means there is a proof of \(S\) in \(\text{PS}\).
If \(S\) is provable, we say \(\text{PS}\) proves \(S\).
We use \(\text{Provable}(\cdot)\) to denote the function such that \(\text{Provable}(\left \langle S \right\rangle)\) returns True if and only if \(S\) is provable. We can view \(\text{Provable}(\cdot)\) as a decision problem.
Statement \(S\) is refutable means \(\text{PS}\) proves the negation of \(S\), (i.e. \({\neg S}\)).
Statement \(S\) is resolvable means that \(S\) is either provable or refutable.
If statement \(S\) is not resolvable, we say \(S\) is independent of \(\text{PS}\).
One can say that the main goal of a proof system is to model truth with provability. So in a sense, the dream is to find a proof system such that for all statements \(S\), \(S\) is true if and only if it is provable, i.e. \(S \leftrightarrow\text{Provable}(\left \langle S \right\rangle)\). Hilbert laid out this dream very explicitly. He challenged mathematicians to come up with such a proof system and prove that it indeed has the desired properties. This is known as Hilbert’s program. We present Hilbert’s program below. But first, we need some definitions.
Let \(\text{PS}\) be a proof system.
\(\text{PS}\) is consistent means for all \(S\), if \(S\) is provable, then \({\neg S}\) is not provable. Or equivalently, for all \(S\), at most one of \(S\) and \({\neg S}\) is provable.
\(\text{PS}\) is sound means for all \(S\), if \(S\) is provable, then \(S\) is true (i.e. \(\text{Provable}(\left \langle S \right\rangle) \to S\)). This is equivalent to saying \(\text{PS}\) does not prove false statements.
\(\text{PS}\) is complete means every statement in \(\text{PS}\) is resolvable. Or equivalently, for all \(S\), at least one of \(S\) and \({\neg S}\) is provable.
\(\text{PS}\) is decidable means that the \(\text{Provable}\) decision problem is decidable.
If \(\text{PS}\) is not consistent, then every statement is provable. To see this, suppose \(S\) is such that both \(S\) and \(\neg S\) are provable. And suppose you want to prove some statement \(T\). Then assume, for the sake of contradiction, \(\neg T\). Then derive \(S\) as well as \(\neg S\) (both are provable). This is the desired contradiction.
If \(\text{PS}\) is sound, then it must be consistent. So we think of soundness as a stronger requirement.
If \(\text{PS}\) is both consistent and complete, then for all statements \(S\), exactly one of \(S\) and \({\neg S}\) is provable.
If \(\text{PS}\) is both sound and complete, then in addition to the observation in the previous point, provable statements would be true. So for all statements \(S\), we would have \(S \leftrightarrow\text{Provable}(\left \langle S \right\rangle)\), and truth would correspond exactly to provability.
It is not hard to see that for any proof system \(\text{PS}\), \(\text{Provable}\) is semi-decidable. Recalling Definition (TM semi-deciding a language or decision problem), to show that \(\text{Provable}\) is semi-decidable, we need to come up with a TM \(M\) such that if \(S\) is provable, \(M(\left \langle S \right\rangle)\) accepts, and if \(S\) is not provable, then \(M(\left \langle S \right\rangle)\) does not accept (i.e. rejects or loops forever). The brute-force search algorithm described below accomplishes this. (Recall \(V\) denotes the verifier for \(\text{PS}\).) \[\begin{aligned} \hline\hline\\[-12pt] &\textbf{def}\;\; M_\text{RESOLVE}(\left \langle S \right\rangle):\\ &{\scriptstyle 1.}~~~~\texttt{For $k = 1, 2, 3, \ldots$}\\ &{\scriptstyle 2.}~~~~~~~~\texttt{For every string $w$ of length $k$:}\\ &{\scriptstyle 3.}~~~~~~~~~~~~\texttt{If $V(\left \langle S, w \right\rangle)$ accepts: return True.}\\ &{\scriptstyle 4.}~~~~~~~~~~~~\texttt{If $V(\left \langle {\neg S}, w \right\rangle)$ accepts: return False.}\\ \hline\hline \end{aligned}\] Note that this is not a decider for \(\text{Provable}\) because it is possible that \(S\) is not resolvable (i.e. independent), and in that case, \(M_\text{RESOLVE}(\left \langle S \right\rangle)\) would loop forever.
Come up with a proof system \(\text{PS}\) that formalizes \(\text{GORM}\), and furthermore:
Prove that \(\text{PS}\) is consistent.
Prove that \(\text{PS}\) is complete.
Prove that \(\text{PS}\) is decidable.
Here is a fun question to think about. In Hilbert’s program, why doesn’t Hilbert ask for a proof of soundness and instead asks for a proof of consistency?
Unfortunately (or perhaps “fortunately” depending on your views), it turns out none of the goals listed above are possible, and we will prove that they are not possible. We currently have everything we need to present the proofs. Starting with the assumption that \(\text{PS}\) is some proof system formalizing \(\text{GORM}\), we can prove that Hilbert’s program for \(\text{PS}\) is not achievable.
That being said, you may be wondering if there is any proof system \(\text{PS}\) that formalizes \(\text{GORM}\). In the next section, we will name such a proof system and mention, at a very high level, some of its parts.
Let \(A\) be some area of mathematics. In order for a proof system to faithfully capture \(\text{GORM}_A\), the best strategy is to mimic \(\text{GORM}_A\).
The general structure of \(\text{GORM}_A\) is that we start with some statements that we assume to be true. We then apply some logical deduction rules to derive new truths. We continue until we derive the statement that we were hoping to prove. Therefore, \(\text{GORM}_A\) has the following elements.
Well-formed statements with some truth value.
Some set of deduction rules that allow you to derive true statements from other true statements.
Some set of axioms (which are well-formed statements) that represent a base layer of assumed truths.
Once we have the 3 pieces above, a proof corresponds to a chain of deduction rules starting from already established truths.
A popular formalization of the above elements uses First Order Logic deductive system.
First Order Logic (FOL) is a general framework that allows us to formally represent well-formed statements with a truth value. In particular, given any area of mathematics, we can specify the elements of the framework so that it matches the area of mathematics we have in mind.
A Hilbert system is a set of deduction rules for the general framework of FOL. Each deduction rule corresponds to a completely syntactic transformation (i.e. each rule is a string manipulation operation). Therefore an application of a deduction rule is easily computable.
An axiomatic system has two parts. First, it is a specific instantiation of FOL capturing some area of mathematics. Second, it has a set of axioms capturing a set of “obvious” truths that, in a sense, characterize that area of mathematics. In particular, the hope is that every true statement in that area is a logical consequence of the axioms.
We require the language \(\{\left \langle S \right\rangle: \text{$S$ is an axiom}\}\) to be decidable. Or in other words, there should be an algorithm to decide, given some statement, whether it is an axiom or not. This, together with the computability of the Hilbert system’s deduction rules, ensure that we have a verifier TM \(V\) as specified in Proof System.
It is worth noting that the set of deduction rules that the Hilbert system specifies is known to be complete (this is Gödel’s Completeness Theorem) in the sense that if you are not able to deduce some truth in the Hilbert System, it is not because you did not have enough deduction rules. It must be because you did not have enough axioms (i.e. some truths were not a logical consequence of the axioms).
Is there an axiomatic system that captures all of \(\text{GORM}\)? Yes, the Zermelo–Fraenkel-Choice (ZFC) axiomatic system for set theory basically captures all mathematical reasoning. Here we will not define ZFC since we won’t need its formal definition. Instead, we will appeal to the following thesis.
Every precise mathematical statement and proof that can be expressed in \(\text{GORM}\) can be expressed using the ZFC axiomatic proof system. In other words, every \(\text{GORM}\)-statement and \(\text{GORM}\)-proof has a corresponding ZFC-statement and ZFC-proof.
Note that the Church-Turing Thesis is really a \(\text{GORA}\)-to-TM thesis, where \(\text{GORA}\) means Good Old Regular Algorithms. It says that any algorithm can be expressed using a TM. Or in other words, every algorithm “compiles down” to a TM.
You should think of \(\text{GORM}\)-to-ZFC Thesis in the same light. Every mathematics proof compiles down to a proof in ZFC.
When we are proving properties of algorithms, we don’t really directly work with TMs, but rather appeal to the Church-Turing Thesis: we work with high-level algorithms with the understanding that they can be translated to TMs. Similarly, when we prove properties of mathematical reasoning, we won’t directly work with ZFC, but appeal to the \(\text{GORM}\)-to-ZFC Thesis: we will use high-level mathematical statements and proofs with the understanding that they can be translated into ZFC statements and proofs.
In this section we will prove Gödel’s Incompleteness theorems. These theorems apply to any proof system \(\text{PS}\) rich enough to formalize basic arguments about TMs. In particular, \(\text{PS}\) does not have to be as rich as ZFC (which captures all mathematical reasoning). Nevertheless, we’ll fix our proof system \(\text{PS}\) to be ZFC, and state our theorems with respect to ZFC. And all the terms defined in Definition (Provable, refutable, resolvable, independent) will be with respect to ZFC.
The 1st Incompleteness theorem, which is philosophically the most important/influential one, turns out to be a relatively straightforward corollary of Turing’s 1st Undecidability Theorem.
Recall that the dream of formalizing mathematics is to be able to model truth with provability. That is, the dream is that for all statements \(S\), we have \(S \leftrightarrow\text{Provable}(\left \langle S \right\rangle)\). We have already observed that this dream is realized for a proof system that is both sound and complete. We will show that this is too good to be true for a proof system like ZFC that is rich enough to reason about TMs. In particular, the existence of undecidable decision problems rules out the dream.
ZFC cannot be both sound and complete. In other words, if ZFC is sound, then it must be incomplete.
The proof is by contradiction, so assume that ZFC is sound and complete. Since ZFC is complete, every statement is resolvable. In addition, since ZFC is sound, the provability of any statement corresponds correctly to its truth value. In other words, for every statement \(S\), we have \(S \leftrightarrow\text{Provable}(\left \langle S \right\rangle)\).
We can say even more though. As we saw in Note (Observations about properties of proof systems), for any proof system, \(M_\text{RESOLVE}\) semi-decides \(\text{Provable}\). For ease of reference, we reproduce the description of \(M_\text{RESOLVE}\): \[\begin{aligned} \hline\hline\\[-12pt] &\textbf{def}\;\; M_\text{RESOLVE}(\left \langle S \right\rangle):\\ &{\scriptstyle 1.}~~~~\texttt{For $k = 1, 2, 3, \ldots$}\\ &{\scriptstyle 2.}~~~~~~~~\texttt{For every string $w$ of length $k$:}\\ &{\scriptstyle 3.}~~~~~~~~~~~~\texttt{If $V(\left \langle S, w \right\rangle)$ accepts: return True.}\\ &{\scriptstyle 4.}~~~~~~~~~~~~\texttt{If $V(\left \langle {\neg S}, w \right\rangle)$ accepts: return False.}\\ \hline\hline\end{aligned}\] In the case of a sound and complete proof system, since there are no independent statements, \(M_\text{RESOLVE}\) always halts and gives the correct answer. So for all \(S\), \(M_\text{RESOLVE}(\left \langle S \right\rangle) \leftrightarrow\text{Provable}(\left \langle S \right\rangle)\). Combining this with our previous observation in the first paragraph, for all statements \(S\), we have \(S \leftrightarrow M_\text{RESOLVE}(\left \langle S \right\rangle)\). This shows that the truth of statements is computable/decidable.
It is now not hard to see that this would allow us to compute/decide undecidable languages, which is the desired contradiction. For instance, the following TM decides \(\overline{\text{SA}_{\text{TM}}}= \overline{\text{SELF-ACCEPTS}_{\text{TM}}}\). \[\begin{aligned} \hline\hline\\[-12pt] &\textbf{def}\;\; M_D(\left \langle M \right\rangle):\\ &{\scriptstyle 1.}~~~~\texttt{Return $M_\text{RESOLVE}(\left \langle \text{``}M(\left \langle M \right\rangle) \text{ does not accept}\text{''} \right\rangle)$.}\\ \hline\hline\end{aligned}\]
The proof above shows us that if ZFC is sound, then there is some statement that is not resolvable (i.e. independent of ZFC). On the other hand, it does not directly give us an explicit independent statement. Our goal now is to find an explicit independent statement.
Let \(M\) be a TM. Define the statement \[S_M = \text{``}M(\left \langle M \right\rangle) \text{ accepts}\text{''}.\] Then the TM \(M_D\) we defined in the proof above has the following equivalent form. \[\begin{aligned} \hline\hline\\[-12pt] &\textbf{def}\;\; M_D(\left \langle M \right\rangle):\\ &{\scriptstyle 1.}~~~~\texttt{Let $S_M$ = "$M(\left \langle M \right\rangle)$ accepts".}\\ &{\scriptstyle 2.}~~~~\texttt{Return not $M_\text{RESOLVE}(\left \langle S_M \right\rangle)$.}\\ \hline\hline\end{aligned}\] So for all \(M\), we have \[M_D(\left \langle M \right\rangle) = \text{not } M_\text{RESOLVE}(\left \langle S_M \right\rangle).\] (When TM \(M_\text{RESOLVE}\) returns True, we say it accepts, and when it returns False, we say it rejects.)
Since \(M_D\) cannot be a correct decider for \(\overline{\text{SA}}\), we know that there exists some TM \(M\) such that \(M_D(\left \langle M \right\rangle)\) does not give the correct answer. And in fact, we already know such an \(M\). Recall the proof of Turing’s 1st Undecidability Theorem where we diagonalized against the set of all TMs. We know that \(M_D\) is a TM and sits somewhere in the table of all TMs.
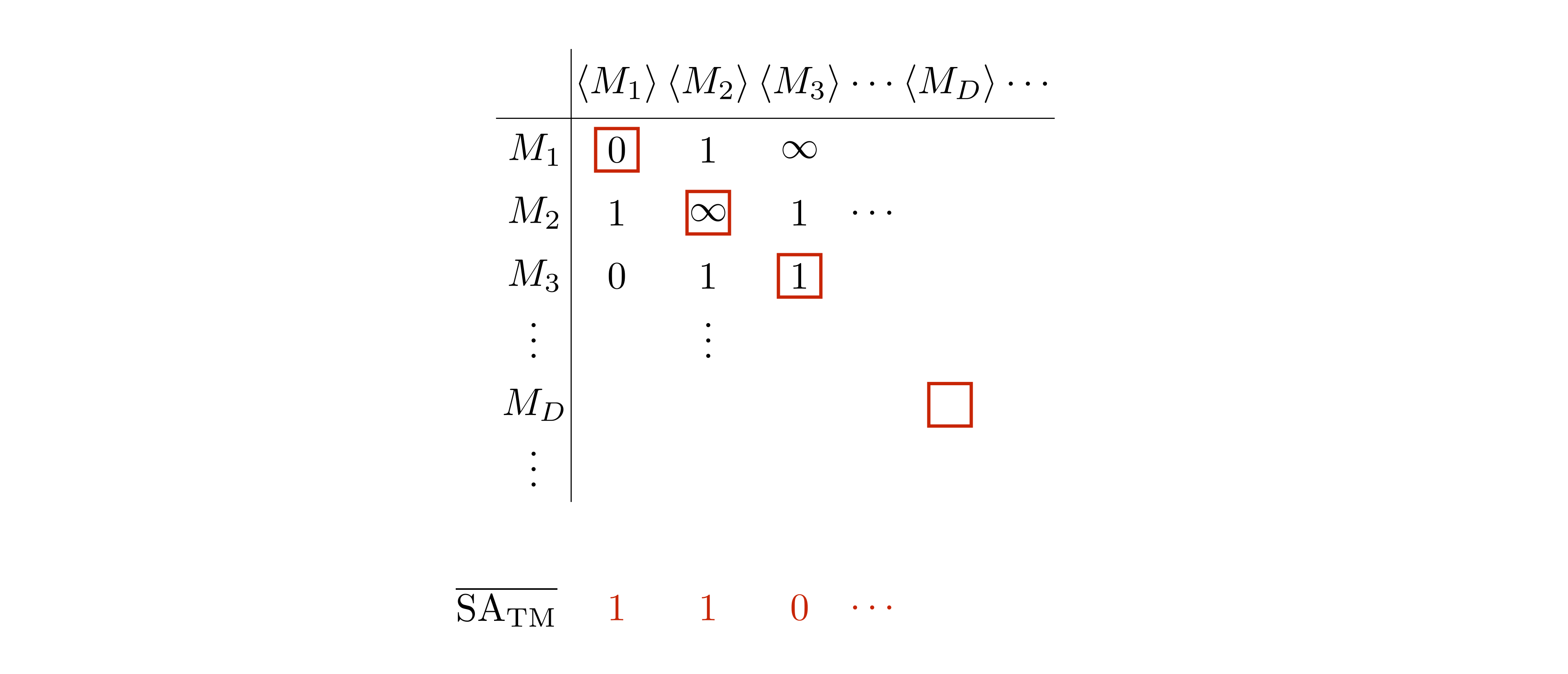
And we know \(M_D\), in attempting to decide \(\overline{\text{SA}}\), does not give the correct answer when the input is \(\left \langle M_D \right\rangle\).
The only reason that \(M_D(\left \langle M_D \right\rangle)\) does not give the correct answer is because \(M_\text{RESOLVE}(\left \langle S_{M_D} \right\rangle)\) does not give the correct answer. With this in mind, there are 2 possibilities for not giving the correct answer.
Case (i): \(M_D(\left \langle M_D \right\rangle)\) loops forever.
In this case \(M_\text{RESOLVE}(\left \langle S_{M_D} \right\rangle)\) loops forever, so \(S_{M_D}\) is not resolvable (i.e. it is independent of ZFC).Case (ii): \(M_D(\left \langle M_D \right\rangle)\) halts.
In this case \(M_\text{RESOLVE}(\left \langle S_{M_D} \right\rangle)\) either returns True or False, but we do not have \(S_{M_D} \leftrightarrow M_\text{RESOLVE}(\left \langle S_{M_D} \right\rangle)\).
In case (ii), ZFC would be unsound with respect to the statement \(S_{M_D}\) because it would be proving a false statement. So if we assume ZFC is sound, we must be in case (i), leading to the following conclusion.
If ZFC is sound, then the statement \(S_{M_D}\) is independent of ZFC.
Now we will relax the assumption “ZFC is sound” to “ZFC is consistent” and show that the above theorem still holds. The strategy will be the same as the one above: we will argue that case (ii) cannot happen, and therefore \(S_{M_D}\) is independent of ZFC.
If we cannot assume that ZFC is sound, then from the fact that a statement \(S\) is provable, we cannot necessarily conclude \(S\) is true, which opens up the possibility of case (ii). This seeming decoupling of provability and truth may be unsettling at first. But just because we have one hand tied behind our back does not mean that ZFC is impossible to reason about. We still have \(\text{GORM}\)-to-ZFC thesis! If there are things we can prove in \(\text{GORM}\), then those things can also be proved in ZFC. And this can provide a nice anchor for us when we reason about ZFC. In particular, even if we cannot assume the soundness of ZFC, we can still argue that there are some specific statements in ZFC that are resolvable and ZFC must be sound with respect to them. The observation below provides such an example, and from it, we’ll be able to quickly conclude that if \(S_{M_D}\) is resolvable, then ZFC must be sound with respect to \(S_{M_D}\).
If \(M\) is a TM such that \(M(x)\) accepts, then the statement \(\text{``}M(x) \text{ accepts}\text{''}\) is provable. Similarly, if \(M(x)\) rejects, then the statement \(\text{``}M(x) \text{ rejects}\text{''}\) is provable.
If a TM \(M\) halts (i.e. either accepts or rejects), then the execution trace of the TM is a proof that it halts. And by GORM-to-ZFC thesis, such a proof also exists in ZFC.
Let \(M\) be a TM such that \(M(x)\) halts. And let \(S = \text{``}M(x) \text{ accepts}\text{''}\). Then if ZFC is consistent, \(S \leftrightarrow M_\text{RESOLVE}(\left \langle S \right\rangle)\) (i.e. ZFC is sound with respect to \(S\)).
If \(S\) is true, then by the previous lemma, \(S\) is provable, and by consistency \(\neg S\) is not provable. So \(M_\text{RESOLVE}(\left \langle S \right\rangle)\) will not find a proof of \(\neg S\) to return False. And it will find a proof of \(S\) to return True.
If \(S\) is false, then since \(M(x)\) halts, we know \(M(x)\) rejects. By the previous lemma, \(\neg S\) is provable, and by consistency \(S\) is not provable. So \(M_\text{RESOLVE}(\left \langle S \right\rangle)\) will not find a proof of \(S\) to return True. And it will find a proof of \(\neg S\) to return False.
Now let’s come back to our goal of ruling out case (ii) above. On the one hand, the description of case (ii) tells us \(M_D(\left \langle M_D \right\rangle)\) halts, and we do not have \(S_{M_D} \leftrightarrow M_\text{RESOLVE}(\left \langle S_{M_D} \right\rangle)\). On the other hand, assuming ZFC is consistent, the above corollary tells us (by plugging in \(M = M_D\) and \(x = \left \langle M_D \right\rangle\)) that \(S_{M_D} \leftrightarrow M_\text{RESOLVE}(\left \langle S_{M_D} \right\rangle)\). Therefore, assuming ZFC is consistent, case (ii) cannot happen, leaving case (i) as the only option.
If ZFC is consistent, then the statement \(S_{M_D}\) is independent of ZFC.
Note that, if a statement \(S\) has the properties
if \(S\) is true, then \(S\) is provable, and
\(S\) is independent (so \(S\) is not provable),
then it must be the case that \(S\) is false. And this is indeed the case for \(S_{M_D}\) assuming ZFC is consistent.
If ZFC is consistent, then \(S_{M_D}\) is false.
We have an explicit statement \(S_{M_D}\) that is independent of ZFC (assuming ZFC is consistent). We can now hope to show that other statements are independent using the following notion of a reduction.
We say proving \(S\) reduces to proving \(T\) (or simply \(S\) reduces to \(T\)) if \(T \to S\) is provable.
Note that if \(S\) reduces to \(T\), and \(T\) is provable, then \(S\) is provable. Or equivalently, if \(S\) reduces to \(T\) and \(S\) is not provable, then \(T\) is not provable.
We already know that \(S_{M_D}\) and \({\neg S_{M_D}}\) are not provable. Therefore, any statement \(T\) that reduces to \(S_{M_D}\) or \({\neg S_{M_D}}\) is not provable. Do we know of any such statement \(T\)? Yes, we do! We just \(\text{GORM}\)-proved for the previous corollary that for \(T =\) “ZFC is consistent”, \(T \to {\neg S_{M_D}}\). And by \(\text{GORM}\)-to-ZFC thesis, \(T \to {\neg S_{M_D}}\) is provable in ZFC.
If ZFC is consistent, then the statement “ZFC is consistent” is not provable in ZFC.
There are at least a couple of tricks you can try to circumvent incompleteness.
Basically no one doubts the consistency of ZFC. So why don’t we add it as an axiom to ZFC? We certainly can. We can call this new axiomatic system \(\text{ZFC}'\). But then we cannot prove that \(\text{ZFC}'\) is consistent. And if we add the consistency of \(\text{ZFC}'\) as an axiom and call the new system \(\text{ZFC}''\), then we cannot prove the consistency of \(\text{ZFC}''\).
Why don’t we define our set of axioms as the set of all true statements? Then surely we would have a complete formal system. The problem is that there would be no algorithm to decide whether a given statement is an axiom or not. And the whole point in trying to formalize mathematics would be defeated.
It is worth noting a very celebrated (but a very difficult) result known as the independence of the continuum hypothesis, which refers to the statement “there is no set \(A\) with \(|\mathbb N| < |A| < |\mathbb R|\)”.
If ZFC is consistent, the continuum hypothesis is independent of ZFC.
What is the upshot of the incompleteness theorems?
We do not doubt that ZFC is sound. And since we believe ZFC captures all mathematical reasoning, we can call a truth attainable if and only if it is provable (in ZFC). Gödel’s Incompleteness theorem says that there are unattainable truths. This highlights the limits of human reasoning, a reality that we have to accept. Furthermore, it suggests that the divide that we should really focus on is attainable truths vs unattainable truths, i.e. provable statements vs unprovable statements.
Note that incompleteness theorems do not rule out the possibility that the decision problem \(\text{Provable}\) is decidable. We only know that if ZFC was complete, then \(M_\text{RESOLVE}\) would be a decider for \(\text{Provable}\). But perhaps even though ZFC is incomplete, \(\text{Provable}\) is still decidable. The last point in Hilbert’s Program expresses the hope that this is true. The question of whether \(\text{Provable}\) is decidable or not is known as Entscheidungsproblem and it was a challenge to the mathematical community posed by Hilbert in 1928. Entscheidungsproblem is German for “decision problem”. And it is apt to think of \(\text{Provable}\) as the decision problem. We will let \(\text{ENT}\) denote the language corresponding to \(\text{Provable}\).
The final blow to Hilbert’s program comes from Alan Turing. In the paper introducing the Turing machine model, he proves the undecidability of \(\text{ENT}\) (and in this course, we call this Turing’s 2nd Undecidability Theorem). This theorem implies that even though we may hope to discover new attainable truths on a case-by-case basis, we cannot hope to have a general algorithm/mechanism that decides all attainable truths.
If ZFC is sound, then \(\text{Provable}\) is undecidable.
To show \(\text{Provable}\) is undecidable, we will show \(\text{HALTS}_{\text{TM}}\) reduces to \(\text{Provable}\). Let \(M_{\text{P}}\) be a decider for \(\text{Provable}\). We construct a decider \(M_{\text{H}}\) for \(\text{HALTS}_{\text{TM}}\) as follows. \[\begin{aligned} \hline\hline\\[-12pt] &\textbf{def}\;\; M_{\text{H}}(\left \langle \text{TM } M, \; \text{string } w \right\rangle):\\ &{\scriptstyle 1.}~~~~\texttt{Let $S$ = "$M(w)$ halts".}\\ &{\scriptstyle 2.}~~~~\texttt{If $M_{\text{P}}(\left \langle S \right\rangle)$ accepts: accept.}\\ &{\scriptstyle 3.}~~~~\texttt{Else: reject.}\\ \hline\hline\end{aligned}\] To see that this is a correct decider for \(\text{HALTS}_{\text{TM}}\), first consider any input \(\left \langle M,w \right\rangle\) such that \(M(w)\) halts. Then by Lemma (Halting statements are provable), \(M_{\text{P}}\) on line 2 will accept, so our decider will accept as well. If \(\left \langle M,w \right\rangle\) is such that \(M(w)\) loops forever, then “\(M(w)\) halts” is false. Since we are assuming ZFC is sound, it does not prove false statements. So “\(M(w)\) halts” is not provable. Therefore, our machine gives the correct answer by rejecting on line 3.
In light of the incompleteness of ZFC (and GORM), it is natural to ask, for which subareas \(A\) of mathematics can we get a sound and complete formalization of \(\text{GORM}_A\). In order to answer this question, we need to specify exactly what we mean by an area \(A\) of mathematics. Here, we will take an abstract/general approach to this. We can think of an area of mathematics as a subset of truths that \(A\) wishes to model and prove. Therefore a nice general definition of \(A\) would simply be a language. Given any language \(L \subseteq \Sigma^*\), we’ll define the set of true statements corresponding to \(L\) as \(A_L = \{\text{``}x \in L\text{''} : x \in L\}\). Then we can think of \(A_L\) as some subset of mathematics (some subset of truths) that we wish to formalize. And we can ask, for which \(L\) can we get a sound and complete formalization of \(A_L\). If a language \(L\) is such that \(A_L\) has a sound and complete formalization, then we’ll say \(L\) is a verifiable language.
Let \(V_\text{ZFC}\) be the verifier TM in the ZFC proof system. A language \(L\) is ZFC-verifiable (or ZFC-provable) if for all \(x \in \Sigma^*\) we have:
(completeness) if \(x \in L\), there exists \(y \in \Sigma^*\) such that \(V_\text{ZFC}(\left \langle \text{``}x \in L\text{''}, y \right\rangle)\) accepts;
(soundness) if \(x \not \in L\), for all \(y \in \Sigma^*\), \(V_\text{ZFC}(\left \langle \text{``}x \in L\text{''}, y \right\rangle)\) rejects.
Note the second point above simply follows from the assumption that ZFC is sound (i.e. the assumption that ZFC does not prove false statements).
In simple terms, a ZFC-verifiable (or ZFC-provable) language is one such that the yes-instances are provable (in ZFC). It is not hard to see that the languages \(\text{SELF-ACCEPTS}_{\text{TM}}\), \(\text{ACCEPTS}_{\text{TM}}\), \(\text{HALTS}_{\text{TM}}\), and \(\text{SAT}_{\text{TM}}\) are all ZFC-verifiable, thanks to Lemma (Halting statements are provable). For instance consider \(\text{ACCEPTS}_{\text{TM}}\). Given \(\left \langle M,x \right\rangle\) such that \(M(x)\) accepts, the execution trace of \(M(x)\) is a proof that \(M(x)\) accepts. Or consider \(\text{SAT}_{\text{TM}}\). Given \(\left \langle M \right\rangle\) such that \(M\) is satisfiable, a proof that \(M\) is satisfiable would consist of a string \(x\) such that \(M(x)\) accepts, together with the execution trace of \(M(x)\).
Not all languages are ZFC-verifiable. And in fact, Gödel’s 1st Incompleteness theorem implies \(\overline{\text{SA}_{\text{TM}}}\) is not ZFC-verifiable since \(\text{``}M_D(\left \langle M_D \right\rangle) \text{ does not accept}\text{''}\) is not provable. In general, we don’t have a way to prove that a TM \(M\), given some input \(x\), loops forever (even though we may be able to prove it for specific instances of \(M\) and \(x\)). Similarly, one can show that given two TMs \(M_1\) and \(M_2\), we don’t have a way to prove whether \(L(M_1) \neq L(M_2)\). So \(\text{NEQ}_{\text{TM}}\) is not ZFC-verifiable either.
Recall that \(\text{ENT}\), the language corresponding to the decision problem \(\text{Provable}\), consists of encodings of all provable statements of ZFC. In a sense, \(\text{ENT}\) is the mother of all ZFC-verifiable languages since \(\text{ENT}\) contains (or encodes), within itself, all ZFC-verifiable languages: for every ZFC-verifiable language \(L\) and for every \(x \in L\), we have \(\left \langle \text{``}x \in L\text{''} \right\rangle \in \text{ENT}\).
A more formal way to say this would be that for any ZFC-verifiable language \(L\), we have \(L \leq_m \text{ENT}\). The reduction is characterized by the transformation \(f : \Sigma^* \to \Sigma^*\) such that \(f(x) = \left \langle \text{``}x \in L\text{''} \right\rangle\). Note that \(f\) is basically trivially computable.
Given that \(\text{ENT}\) is a ZFC-verifiable language (follows immediately from the definitions), we can say that \(\text{ENT}\) is the “hardest” language among all ZFC-verifiable languages. And in such cases, computer scientists like to use the word “complete”, so we say that \(\text{ENT}\) is complete for the set of all ZFC-verifiable languages.
The essence of mathematics is that it is a certain kind of computation. And we model this computation by a deductive proof system. In a deductive proof system, correctness of the verification process rests on the assumption that the axioms are correct.
It is natural to generalize a deductive proof system so that we do not restrict ourselves to only certain kind of computations (i.e. a sequence of deductions starting from the axioms), but rather allow any kind of computation as a possible verification process.
Let \(V\) be a decider TM and let \(L\) be a language over \(V\)’s input alphabet \(\Sigma\). We say that \(V\) verifies \(L\) if for all \(x \in \Sigma^*\) the following holds:
(completeness) if \(x \in L\), there exists \(y \in \Sigma^*\) such that \(V(\left \langle x, y \right\rangle)\) accepts;
(soundness) if \(x \not \in L\), for all \(y \in \Sigma^*\), \(V(\left \langle x, y \right\rangle)\) rejects.
We call \(V\) a verifier for \(L\). We also call (and think of) \(V\) as computational proof system for \(L\).
For notational convenience, we will write \(V(x,y)\) to denote \(V(\left \langle x, y \right\rangle)\) and think of \(V\) as a TM with two separate inputs, one for the instance \(x\) of the problem/language \(L\), and one for the “proof” \(y\).
A language \(L\) is called verifiable if there exists a TM that verifies \(L\).
\(\text{SELF-ACCEPTS}_{\text{TM}}\), \(\text{ACCEPTS}_{\text{TM}}\), \(\text{HALTS}_{\text{TM}}\), and \(\text{SAT}_{\text{TM}}\) are all verifiable. We encourage you to think of verifiers for each of these languages. Here we’ll present one for \(\text{ACCEPTS}_{\text{TM}}\). \[\begin{aligned} \hline\hline\\[-12pt] &\textbf{def}\;\; V(\left \langle \text{TM } M, \; \text{string } x \right\rangle,\; \left \langle \text{natural } k \right\rangle):\\ &{\scriptstyle 1.}~~~~\texttt{Simulate $M(x)$ for $k$ steps.}\\ &{\scriptstyle 2.}~~~~\texttt{If it accepts, accept.}\\ &{\scriptstyle 3.}~~~~\texttt{Else, reject.}\\ \hline\hline\end{aligned}\] Note that \(V\) is indeed a decider. To see that it is a correct verifier for \(\text{ACCEPTS}_{\text{TM}}\), first assume that \(M(x)\) accepts. Let \(t\) be the number of steps \(M(x)\) takes to accept. Then \(V(\left \langle M, x \right\rangle, \left \langle t \right\rangle)\) simulates \(M(x)\) for \(t\) steps and accepts on line 2.
Now assume \(M(x)\) does not accept. In this case we must argue that for all natural numbers \(k\), \(V(\left \langle M, x \right\rangle, \left \langle k \right\rangle)\) rejects. And this is indeed the case because no matter what \(k\) is, the simulation on line 1 does not result in \(M(x)\) accepting. And so \(V(\left \langle M, x \right\rangle, \left \langle k \right\rangle)\) rejects on line 3.
One can intuitively think of a verifiable language as one that can be decided with a certain kind of “help” (help that you don’t have to necessarily trust and can verify yourself). In comparison, a decidable language is one that can be decided with no help. Therefore every decidable language is verifiable (see the exercise below). On the other hand, there are verifiable languages (like \(\text{ACCEPTS}_{\text{TM}}\), \(\text{HALTS}_{\text{TM}}\), \(\text{SAT}_{\text{TM}}\)) that are not decidable.
A natural question at this point is whether every language is verifiable. Consider, say, \(\overline{\text{HALTS}_{\text{TM}}}\). Is there always a way to computationally prove that a TM \(M\), on input \(x\), does not halt? The next theorem will give us a better understanding of computational verifiability and allow us to answer this question.
Prove that every decidable language is verifiable.
Let \(L\) be a decidable language and let \(M\) be a decider for it. We want to show that \(L\) is verifiable, so we need to construct a verifier TM \(V\) that satisfies the conditions laid out in Definition (Computational proof system). Here is the description of a verifier for \(L\). \[\begin{aligned} \hline\hline\\[-12pt] &\textbf{def}\;\; V(x, y):\\ &{\scriptstyle 1.}~~~~\texttt{Run $M(x)$.}\\ &{\scriptstyle 2.}~~~~\texttt{If it accepts, accept.}\\ &{\scriptstyle 3.}~~~~\texttt{It if rejects, reject.}\\ \hline\hline\end{aligned}\] Note that since \(M\) is a decider, \(V\) is also a decider. To see that \(V\) is a correct verifier for \(L\), first consider the case \(x \in L\). Then since \(M\) is a correct decider for \(L\), \(M(x)\) accepts. So no matter what \(y\) is (i.e. for all \(y\)), \(V(x,y)\) accepts. Therefore the completeness condition of the verifier is satisfied.
Now consider the case \(x \not \in L\). Once again, since \(M\) is a correct decider for \(L\), \(M(x)\) rejects. So for all \(y\), \(V(x,y)\) rejects. Therefore the soundness condition of the verifier is satisfied.
A language \(L\) is verifiable if and only if it is semi-decidable. Or in other words, \(\mathsf{RE}\) is the set of all verifiable languages.
We have two directions to prove. Let’s first assume \(L\) is a verifiable language. And let \(V\) be a verifier for \(L\). We want to show that \(L\) is semi-decidable. We will do so by presenting a semi-decider \(M\) for \(L\) that makes use of \(V\). Here is the semi-decider for \(L\). \[\begin{aligned} \hline\hline\\[-12pt] &\textbf{def}\;\; M(x):\\ &{\scriptstyle 1.}~~~~\texttt{For $k = 0, 1, 2, 3, \ldots$}\\ &{\scriptstyle 2.}~~~~~~~~\texttt{For every string $y$ of length $k$:}\\ &{\scriptstyle 3.}~~~~~~~~~~~~\texttt{If $V(\left \langle x, y \right\rangle)$ accepts: accept.}\\ \hline\hline\end{aligned}\] To see that this is a correct semi-decider for \(L\), note that if the input \(x\) is such that \(x \in L\), since \(L\) is verifiable, we know there exists some \(y \in \Sigma^*\) such that \(V(\left \langle x, y \right\rangle)\) accepts. The TM \(M\) does a brute-force search over all possible strings, so it will eventually find this \(y\), and on line 3, it will accept. If on the other hand the input \(x\) is such that \(x \not \in L\), then we know that for all \(y\), \(V(\left \langle x,y \right\rangle)\) rejects, therefore \(M(x)\) can never accept (i.e. loops forever).
For the other direction, we will assume \(L\) is semi-decidable and show that it must be verifiable. Let \(M\) be a TM that semi-decides \(L\). To show that \(L\) is verifiable, we will construct a verifier \(V\) for \(L\) by making use of \(M\). The description of the verifier is as follows. \[\begin{aligned} \hline\hline\\[-12pt] &\textbf{def}\;\; V(x,\; \left \langle \text{natural } k \right\rangle):\\ &{\scriptstyle 1.}~~~~\texttt{Simulate $M(x)$ for $k$ steps.}\\ &{\scriptstyle 2.}~~~~\texttt{If it accepts, accept.}\\ &{\scriptstyle 3.}~~~~\texttt{Else, reject.}\\ \hline\hline\end{aligned}\] Note that \(V\) is indeed a decider. To see that it is is a correct verifier, first assume that \(x \in L\). Then we know \(M(x)\) accepts. Let \(t\) be the number of steps \(M(x)\) takes to accept. Then \(V(x, \left \langle t \right\rangle)\) will simulate \(M(x)\) for \(t\) steps and accept on line 2.
Now assume \(x \not \in L\). In this case we must argue that for all natural numbers \(k\), \(V(x, \left \langle k \right\rangle)\) rejects. Since \(x\) is not in \(L\), we know that \(M(x)\) does not accept. Therefore no matter what \(k\) is, the simulation on line 1 will not result in \(M(x)\) accepting. And so \(V(x, \left \langle k \right\rangle)\) will reject on line 3.
Recall that we started this chapter with the observation that GORM can be thought of as the following two computational processes.
A prover basically searches for a proof that the verifier would accept.
In this section we have generalized the above by allowing the human to be any computation/TM. The definition of verifiability formalizes the computational \(\text{Verifier}\). And one can view the definition of semi-decidability as a formalization of the computational \(\text{Prover}\). In the proof of Theorem (Verifiability is equivalent to semi-decidability), we set up the semi-decider \(M\) so that it searches for a proof that the verifier would accept. And in general, one can think of any semi-decider \(M\) for \(L\) as attempting to generate a proof of \(x \in L\): If \(M\) accepts \(x\), then the execution of \(M(x)\) is itself a proof that \(x \in L\).
In this setting, the equivalence of Verifier and Prover is a consequence of the fact that so far, our models do not take into consideration computational complexity at all. And in fact, this is a main limitation of our approach so far. In practice and intuitively, there seems to be a big difference between coming up with a proof and verifying a proof. This distinction is one of the most fundamental distinctions in the study of computation. And to understand it, we will next move to the second part of the course and start the study of computational complexity.